O(n²): 冒泡排序、选择排序、插入排序
O(nlogn): 归并排序、快速排序、堆排序
O(n): 计数排序、桶排序、基数排序

1. 冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求，如果不满足就让它俩互换。一次冒泡至少会让一个元素移动到它应在的位置，重复 n 次，就完成了 n 个数据的排序工作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const arr = [4,5,6,3,2,1]   // 第一次遍历后，至少6会在正确的位置上
const bubbleSort = arr => {
  if (arr.length <= 1) return arr
  
  for (let i = 0; i < arr.length - 1; i++) {
    let hasChange = false
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        const temp = arr[j]
        arr[j] = arr[j + 1]
        arr[j + 1] = temp
        hasChange = true
      }
    }
    if (!hasChange) break
  }

  return arr
}

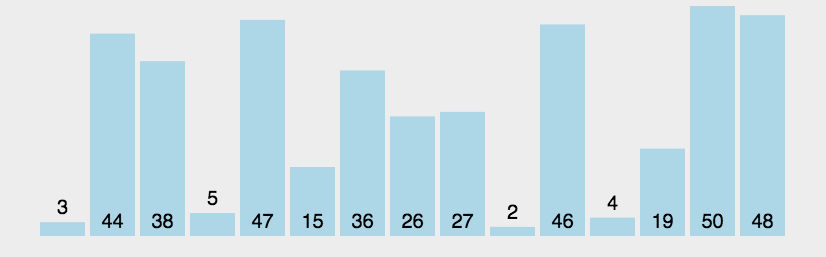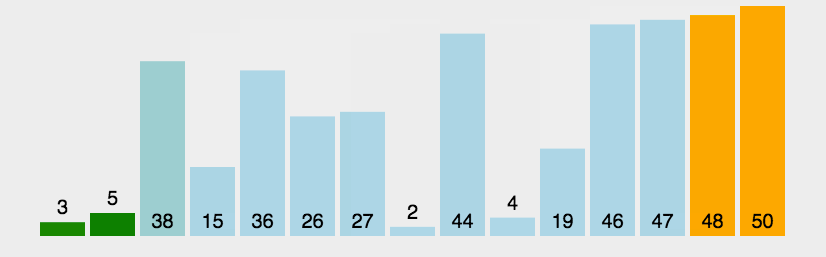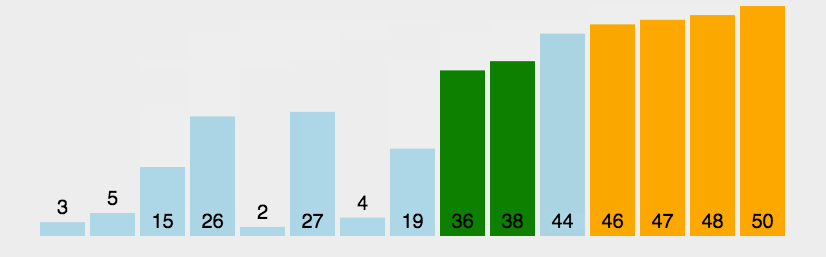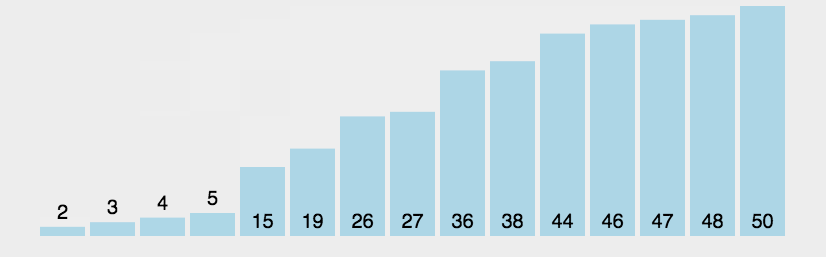
2. 选择排序

选择排序把数组中的数据分成前后两个区间，已排序区间和未排序区间。在未排序区间里找到最小元素，存放到已排序序列的末尾，以此类推，直到所有元素均排序完毕。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
const selectionSort = arr => {
  for (let i = 0; i < arr.length; i++) {
    let minIndex = i
    for (let j = i; i < arr.length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j
      }
    }
    const temp = arr[i]
    arr[i] = arr[minIndex]
    arr[minIndex] = temp
  }
  return arr
}

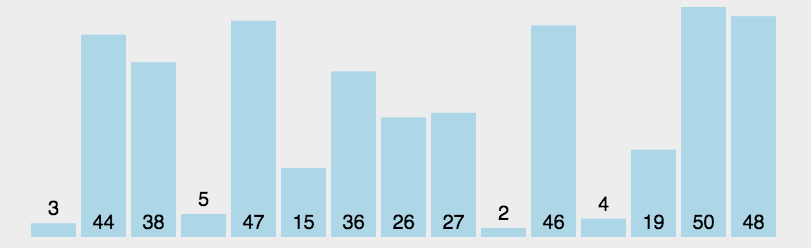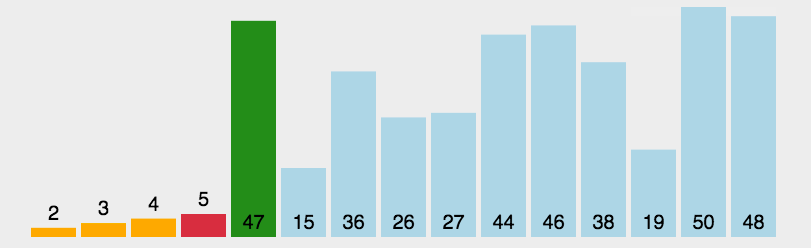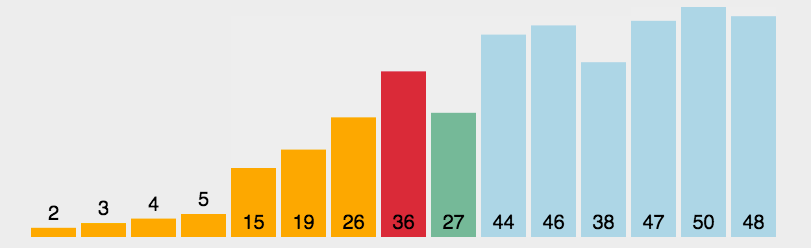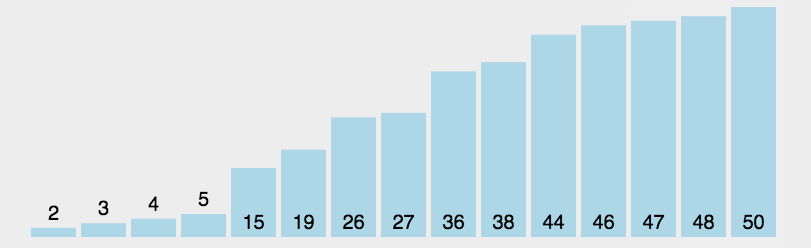
3. 插入排序

插入排序将数组中的数据分为前后两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。然后取未排序区间中的第一个元素，在已排序区间中找到合适的位置插入。

1
2
3
4
5
6
7
8
9
10
11
12
13
const arr = [4,5,6,3,2,1]
const insertSort = arr => {
  for (let i = 1; i < arr.length; i++) {
    preIndex = i - 1
    current = arr[i]
    while (arr[preIndex] > current && preIndex > 0) {
      arr[preIndex + 1] = arr[preIndex]
      preIndex--
    }
    arr[preIndex + 1] = current
  }
  return arr
}

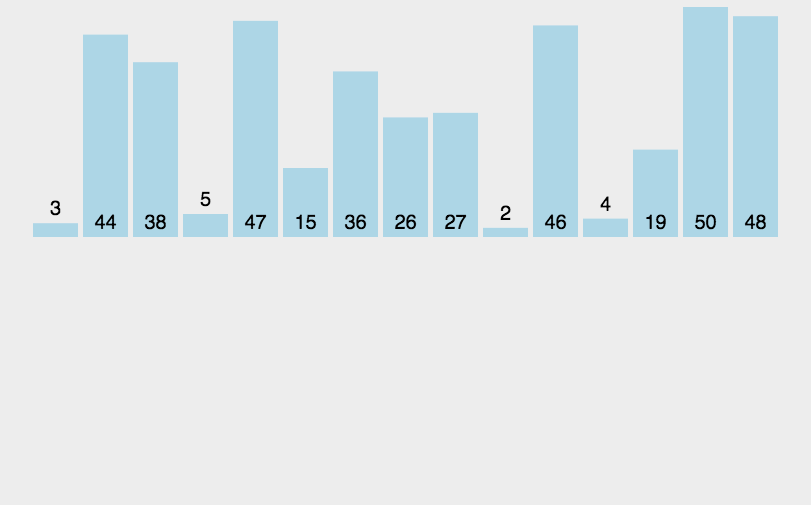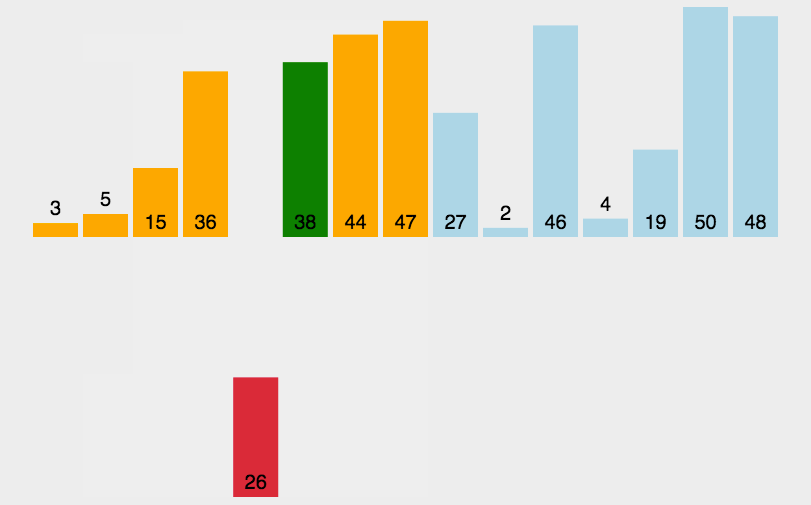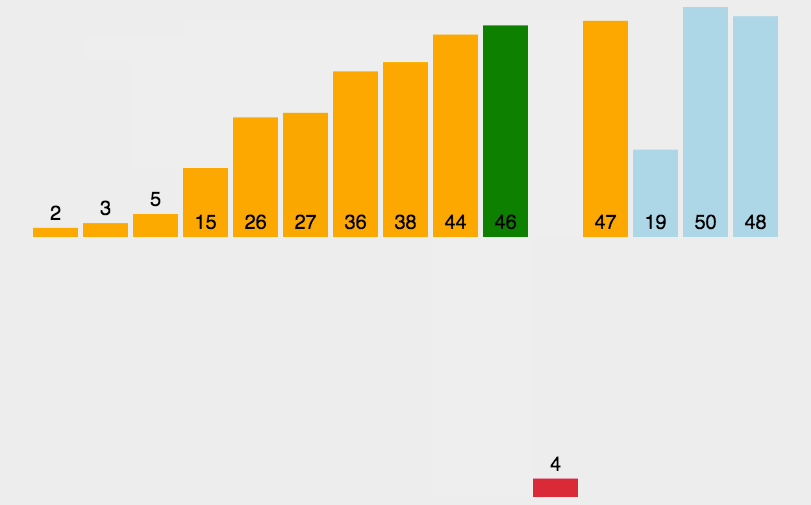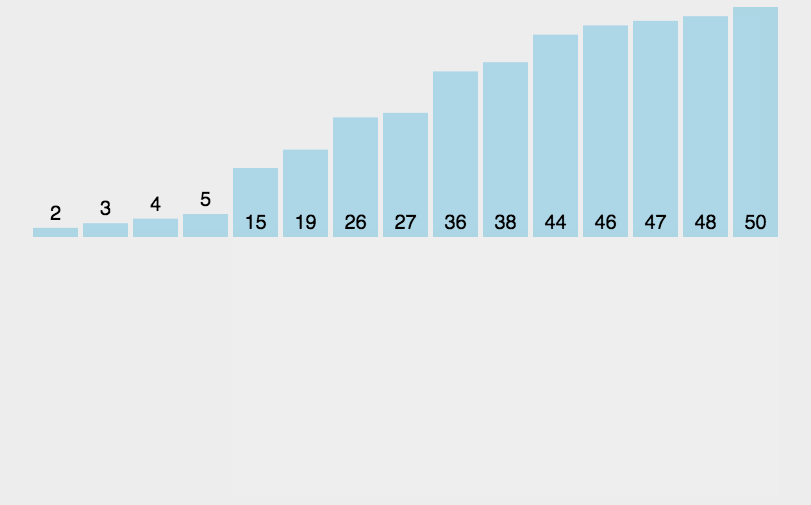
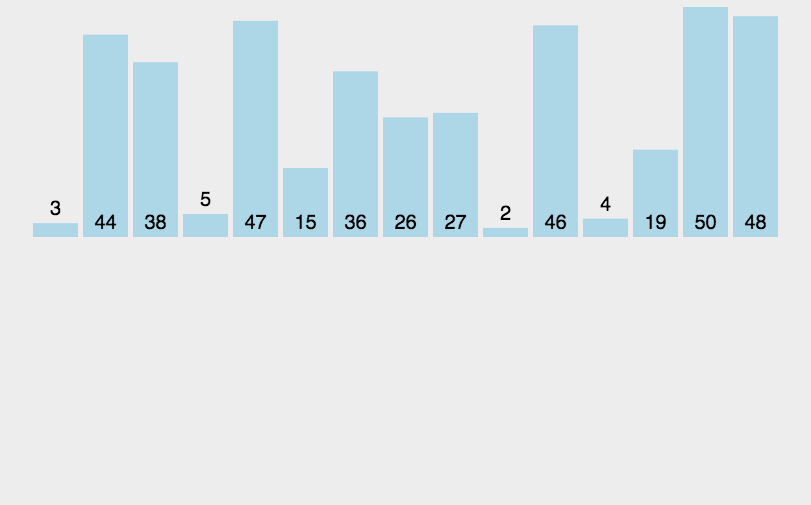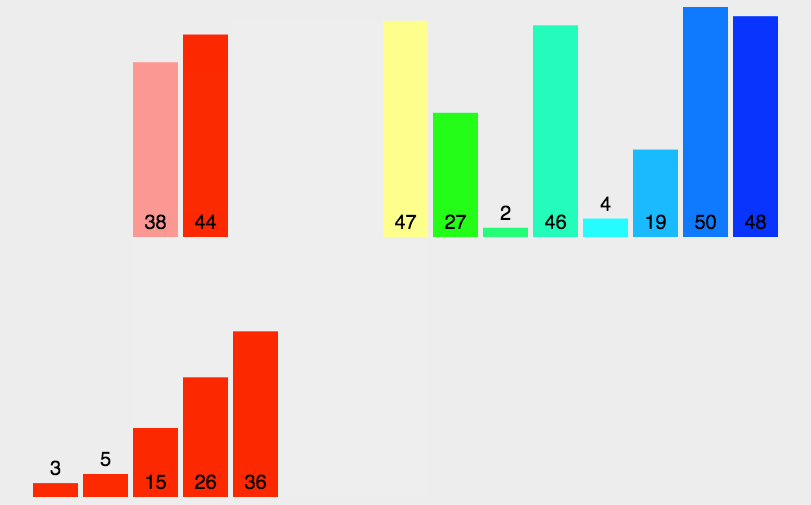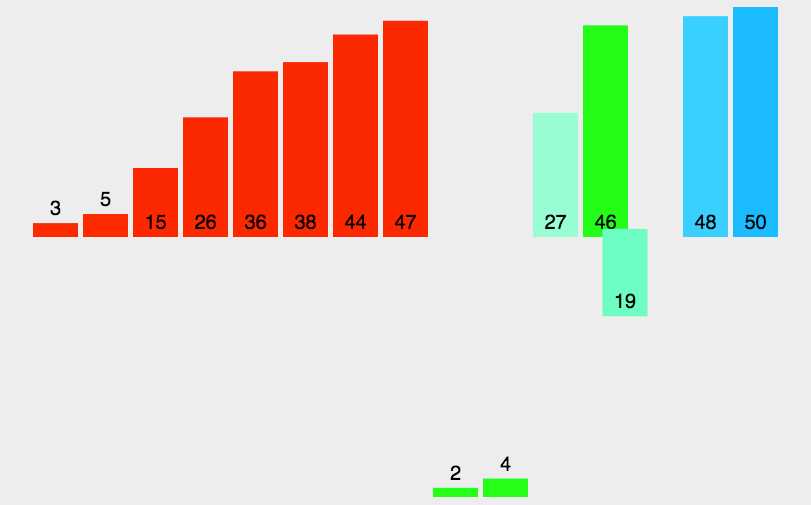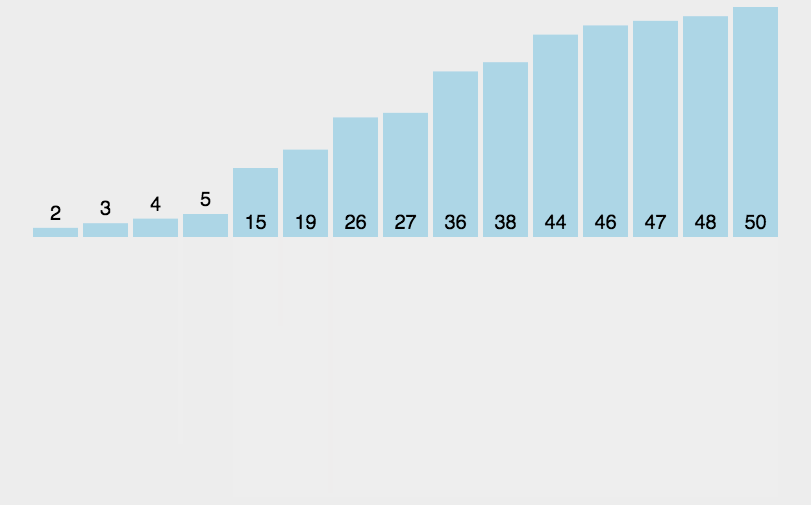
4. 归并排序

将已有序的子序列合并，得到完全有序的序列。再将两个有序的数组合并成一个有序的数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function mergeSort (arr) {
  const len = arr.length
  if (len < 2) return arr
  
  const mid = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle)

  return merge(mergeSort(left), mergeSort(right))
}

function merge (left, right) {
  const result = []
  while (left.length > 0 && right.length > 0) {
    if (left[0] < right[0]) {
      result.push(left.shift())
    } else {
      result.push(right.shift())
    }
  }
  while (left.length) {
    result.push(left.shift())
  }
  while (right.length) {
    result.push(right.shift())
  }
  return result
}

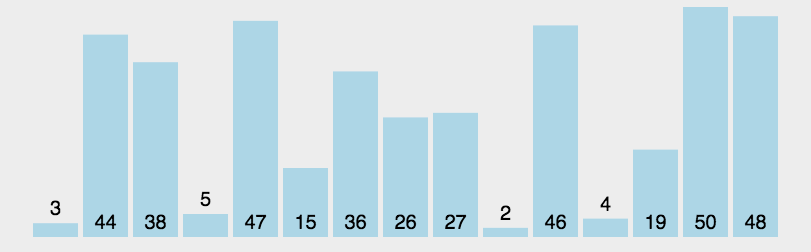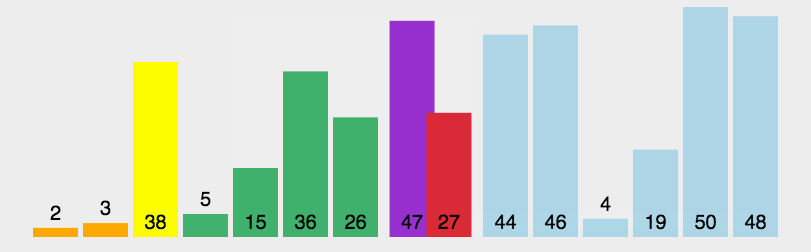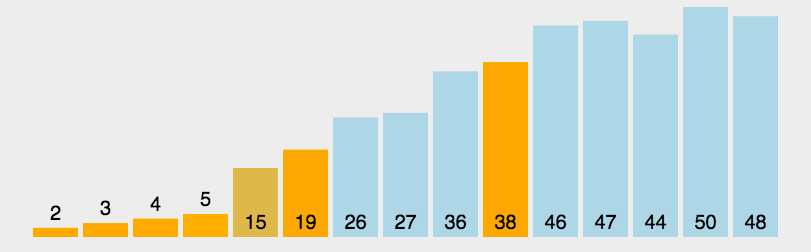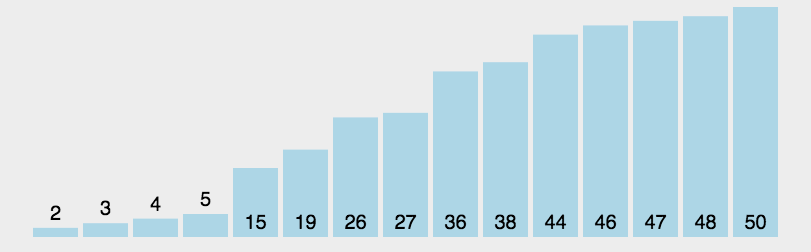
5. 快速排序

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 privot (分区点)。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function quickSort (arr, left, right) {
  left = typeof left !== 'number' ? 0 : left,
  right = typeof right !== 'number' ? arr.length - 1 : right

  debugger
  if (left < right) {
    const partitionIndex = partition(arr, left, right)
    quickSort(arr, left, partitionIndex - 1)
    quickSort(arr, partitionIndex + 1, right)
  }
  return arr
}

function partition(arr, left, right) {
  let pivot = left, // 基准点
      index = pivot + 1
  for (let i = index; i <= right; i++) {
    if (arr[i] < arr[pivot]) {
      swap(arr, i, index)
      index++
    }
  }
  
  return index - 1
}


function swap(arr, i, j) {
  const temp = arr[i]
  arr[i] = arr[j]
  arr[j] = temp
}

6. 堆排序

大顶堆和小顶堆，就是我们想要的数据结构。它总是保持着堆顶元素是最大/最小的。这里假设我们已经实现了大顶堆和小顶堆，它允许初始化一个数组，对数组中的元素进行堆排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
varlen;   // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量
 
function buildMaxHeap(arr) {  // 建立大顶堆
  len = arr.length;
  for(var i = Math.floor(len/2); i >= 0; i--) {
    heapify(arr, i);
  }
}
 
function heapify(arr, i) {    // 堆调整
  var left = 2 * i + 1,
      right = 2 * i + 2,
      largest = i;

  if(left < len && arr[left] > arr[largest]) {
    largest = left;
  }

  if(right < len && arr[right] > arr[largest]) {
    largest = right;
  }

  if(largest != i) {
    swap(arr, i, largest);
    heapify(arr, largest);
  }
}
 
function swap(arr, i, j) {
  vartemp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}
 
function heapSort(arr) {
  buildMaxHeap(arr);

  for(vari = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i);
    len--;
    heapify(arr, 0);
  }
  returnarr;
}

7. 计数排序

计数排序要求输入的数据必须是有确定范围的整数。其核心是将输入的数据值化为键存储在数组中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function countingSort (arr, maxValue) {
  const bucket = new Array(maxValue + 1)
  let sortedIndex = 0
  for (let i = 0; i < arr.length; i++) {
    if (bucket[arr[i]]) {
      bucket[arr[i]] = 0
    }
    bucket[arr[i]]++
  }

  for (let i = 0; i < bucket.length; i+) {
    while (bucket[i] > 0) {
      arr[sortedIndex] = j
      sortedIndex++
      bucket[j]--
    }
  }
  return arr
}

8. 桶排序

假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序。

9. 基数排序

参考资料